DECIMAL Storage

The database server uses one byte of disk storage to store two digits of a decimal number, plus an additional byte to store the exponent and sign, with the first byte representing a sign bit and a 7-bit exponent in excess-65 format. The rest of the bytes express the mantissa as base-100 digits. The significant digits to the left of the decimal and the significant digits to the right of the decimal are stored in separate groups of bytes. At the maximum precision specification, DECIMAL(32,s) data types can store s-1 decimal digits to the right of the decimal point, if s is an odd number.

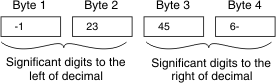
How the database server stores decimal numbers is illustrated in the following example. If you specify DECIMAL(6,3), the data type consists of three significant digits in the integral part and three significant digits in the fractional part (for instance, 123.456). The three digits to the left of the decimal are stored on 2 bytes (where one of the bytes only holds a single digit) and the three digits to the right of the decimal are stored on another 2 bytes, as Schematic that illustrates the storage of digits in a decimal (p,s) value illustrates.

(The exponent byte is not shown.) With the additional byte required for the exponent and sign, DECIMAL(6,3) requires a total of 5 bytes of storage.

Four rectangles depict 4 bytes that store a "123.456" value. First 2 bytes store the integer part (123), with "23" in the 2nd byte. Last 2 bytes store the fractional part (456), with "45" in 3rd byte. End figure description — Figure 1: Schematic that illustrates the storage of digits in a decimal (p,s) value

You can use the following formulas (rounded down to a whole number of bytes) to calculate the byte storage (N) for a DECIMAL(p,s) data type (where N includes the byte that is required to store the exponent and the sign):

If the scale is odd: N = (precision + 4) / 2
If the scale is even: N = (precision + 3) / 2

For example, the data type DECIMAL(5,3) requires 4 bytes of storage (9/2 rounded down equals 4).

There is one caveat to these formulas. The maximum number of bytes the database server uses to store a decimal value is 17. One byte is used to store the exponent and sign, leaving 16 bytes to store up to 32 digits of precision. If you specify a precision of 32 and an odd scale, however, you lose 1 digit of precision. Consider, for example, the data type DECIMAL(32,31). This decimal is defined as 1 digit to the left of the decimal and 31 digits to the right. The 1 digit to the left of the decimal requires 1 byte of storage. This leaves only 15 bytes of storage for the digits to the right of the decimal. The 15 bytes can accommodate only 30 digits, so 1 digit of precision is lost.