Description of WKBGeometry byte streams
The well-known binary representation for geometry is described
below. The basic building block is the byte stream for a point that
consists of two doubles. The byte streams for other geometries are
built using the byte streams for geometries that have already been
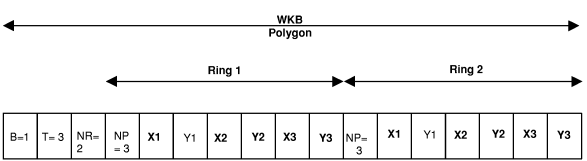
defined. Figure 1: Well-known
binary representation for a geometry object in NDR format(B=1) of
type polygon (T=3) with two rings (NR = 2) and each ring having three
points (NP = 3)
Important: These structures are only intended
to define the stream of bytes that is transmitted between the client
and server. They should not be used as C-language data structures.
See the following figure for an example of such a byte stream.
// Basic Type definitions
// byte : 1 byte
// uint32 : 32 bit unsigned integer (4 bytes)
// double : double precision number (8 bytes)
// Building Blocks : Point, LinearRing
Point {
double x;
double y;
double z;
double m;
};
LinearRing {
uint32 numPoints;
Point points[numPoints];
}
enum wkbGeometryType {
wkbPoint = 1,
wkbLineString = 2,
wkbPolygon = 3,
wkbMultiPoint = 4,
wkbMultiLineString = 5,
wkbMultiPolygon = 6,
wkbGeometryCollection = 7,
wkbPointZ = 1001,
wkbLineStringZ = 1002,
wkbPolygonZ = 1003,
wkbMultiPointZ = 1004,
wkbMultiLineStringZ = 1005,
wkbMultiPolygonZ = 1006,
wkbGeometryCollectionZ = 1007,
wkbPointM = 2001,
wkbLineStringM = 2002,
wkbPolygonM = 2003,
wkbMultiPointM = 2004,
wkbMultiLineStringM = 2005,
wkbMultiPolygonM = 2006,
wkbGeometryCollectionM = 2007,
wkbPointZM = 3001,
wkbLineStringZM = 3002,
wkbPolygonZM = 3003,
wkbMultiPointZM = 3004,
wkbMultiLineStringZM = 3005,
wkbMultiPolygonZM = 3006,
wkbGeometryCollectionZM = 3007
};
enum wkbByteOrder {
wkbXDR = 0, // Big Endian
wkbNDR = 1 // Little Endian
};
WKBPoint {
byte byteOrder;
uint32 wkbType; // 1
Point point;
}
WKBLineString {
byte byteOrder;
uint32 wkbType; // 2
uint32 numPoints;
Point points[numPoints];
}
WKBPolygon {
byte byteOrder;
uint32 wkbType; // 3
uint32 numRings;
LinearRing rings[numRings];
}
WKBMultiPoint {
byte byteOrder;
uint32 wkbType; // 4
uint32 num_wkbPoints;
WKBPoint WKBPoints[num_wkbPoints];
}
WKBMultiLineString {
byte byteOrder;
uint32 wkbType; // 5
uint32 num_wkbLineStrings;
WKBLineString WKBLineStrings[num_wkbLineStrings];
}
wkbMultiPolygon {
byte byteOrder;
uint32 wkbType; // 6
uint32 num_wkbPolygons;
WKBPolygon wkbPolygons[num_wkbPolygons];
}
WKBGeometry {
union {
WKBPoint point;
WKBLineString linestring;
WKBPolygon polygon;
WKBGeometryCollection collection;
WKBMultiPoint mpoint;
WKBMultiLineString mlinestring;
WKBMultiPolygon mpolygon;
}
};
WKBGeometryCollection {
byte byte_order;
uint32 wkbType; // 7
uint32 num_wkbGeometries;
WKBGeometry wkbGeometries[num_wkbGeometries]
}
The number of bytes in each box is shown in the following
table.
| Ring | Box | Bytes |
|---|---|---|
| B=1 | 1 | |
| T=3 | 4 | |
| NR=2 | 4 | |
| 1 | NP=3 | 4 |
| 1 | X1 | 8 |
| 1 | Y1 | 8 |
| 1 | X2 | 8 |
| 1 | Y2 | 8 |
| 1 | X3 | 8 |
| 1 | Y3 | 8 |
| 2 | NP=3 | 4 |
| 2 | X1 | 8 |
| 2 | Y1 | 8 |
| 2 | X2 | 8 |
| 2 | Y2 | 8 |
| 2 | X3 | 8 |
| 2 | Y3 | 8 |